作者: Burton H. Bloom
本文分析了哈希编码中某些计算因素之间的权衡。所考虑的范例问题是逐一测试一系列消息是否属于给定消息集。研究了两种新的哈希编码方法,并将其与一种特定的传统哈希编码方法进行了比较。考虑的计算因素包括哈希区域的大小(空间)、识别消息不属于给定集合所需的时间(拒绝时间)和允许的错误频率。
新方法旨在减少包含哈希编码信息所需的空间量,而不是与传统方法相关联的空间量。减少空间是通过利用在某些应用中可能容忍一小部分委托错误的可能性来实现的,特别是在涉及大量数据且因此使用传统方法不可行核心常驻哈希区域的应用中。
在这样的应用中,可以设想通过使用较小的核心常驻哈希区域与新方法结合使用,并在必要时使用一些次要的,可能耗时的测试来“捕获”与新方法相关联的一小部分错误,可以提高整体性能。讨论了一个例子,说明了新方法可能的应用领域。
对范例问题的分析表明,允许少量测试消息被错误地识别为给定集合的成员,将允许使用更小的哈希区域,而不会增加拒绝时间。
关键词和短语: 哈希编码、哈希寻址、散列存储、搜索、存储布局、检索权衡、检索效率、存储效率 CR 类别: 3.73、3.74、3.79
导言 #
在传统的哈希编码中,哈希区域被组织成单元,并且使用迭代伪随机计算过程从给定的消息集中生成空单元的哈希地址,然后将消息存储到这些单元中。通过类似的迭代生成单元哈希地址的过程来测试消息。然后将这些单元的内容与测试消息进行比较。匹配表示测试消息是集合的成员;空单元表示相反。假设读者熟悉这种方法和类似的传统哈希编码方法 [1, 2, 3]。
将引入的新哈希编码方法建议用于绝大多数要测试的消息不属于给定集合的应用程序。对于这些应用程序,将考虑将识别测试消息不属于给定集合所需的平均时间(称为拒绝时间)作为时间单位。此外,由于通常可以通过检查部分消息来识别单元的内容与测试消息不匹配,因此将引入一个适当的假设,即访问哈希区域中各个位所需的时间。
除了两个计算因素(拒绝时间和空间(即哈希区域大小))之外,本文还考虑了第三个计算因素,即允许的错误分数。将表明,允许少量测试消息被错误地识别为给定集合的成员,将允许使用更小的哈希区域,而不会增加拒绝时间。在一些实际应用中,哈希区域大小的这种减少可能导致在核心(其中可以快速处理哈希区域)中维护哈希区域与将其放在慢速访问的批量存储设备(例如磁盘)上的区别。
将介绍两种通过允许错误来减少哈希区域大小的方法。将分析每种方法的哈希区域大小和允许错误分数之间的权衡,以及它们产生的空间/时间权衡。
读者应该注意,新方法并不用于替代任何当前使用哈希编码的应用领域的传统哈希编码方法(例如,符号表管理 [1])。相反,它们旨在使利用哈希编码技术在某些领域成为可能,在这些领域中,传统的无错误方法需要太大的哈希区域,无法成为核心常驻,因此被认为是不可行的。为了在不引入过多的拒绝时间的情况下大幅减少哈希区域大小,牺牲了与传统方法相关的无错误性能。在无错误性能是必需的应用领域,这些新方法不适用。
一个示例应用程序 #
允许错误有望允许有效减少哈希区域大小的应用程序类型可以描述如下。假设程序必须针对大量不同情况执行计算过程。此外,假设对于绝大多数情况,该过程非常简单,但对于难以识别的一小部分情况,该过程非常复杂。然后,对少数情况的标识符进行哈希编码可能很有用,以便可以更轻松地测试要处理的每个情况是否属于少数情况集。如果一个特定情况被拒绝(大多数情况下会发生这种情况),则将使用简单的过程。如果一个案例没有被拒绝,那么可以对其进行后续测试,以确定它实际上是少数情况集的成员还是“允许的错误”。通过允许此类错误,可以使哈希区域足够小,从而使此过程切实可行。
作为这种应用程序的一个示例,请考虑一个自动连字符程序。让我们假设一些简单的规则可以正确地连字符 90% 的英语单词,但其他 10% 需要字典查找。假设这个字典太大而无法放入可用的核心内存中,因此将其保存在磁盘上。通过允许一些单词被错误地识别为属于 10%,可以使 10% 的哈希区域足够小,以适合核心。当出现“允许的错误”时,测试词不会在磁盘上找到,可以使用简单的规则对其进行连字符。很少发生不必要的磁盘访问,其频率与核心常驻哈希区域的大小有关。本文末尾将详细分析此示例应用程序。
传统哈希编码方法 #
作为出发点,我们将回顾一种不允许出现错误的传统哈希编码方法。假设我们存储一组 n 条消息,每条消息长度为 b 位。首先,我们将哈希区域组织成 h 个单元,每个单元 b + 1 位,h > n。每个单元中的额外位用作标志,以指示该单元是否为空。为此,将消息视为 b + 1 位对象,第一位始终设置为 1。然后,存储过程如下:
生成一个称为哈希地址的伪随机数,例如 k,(0 ≤ k ≤ h - 1),其方式取决于正在考虑的消息。然后检查第 k 个单元以查看它是否为空。如果是,则将消息存储在第 k 个单元中。如果不是,则继续生成其他哈希地址,直到找到一个空单元,然后将消息存储到该单元中。
测试新消息是否为成员的方法类似于存储消息的方法。使用与上述相同的随机数生成技术生成一系列哈希地址,直到发生以下情况之一。
- 找到一个单元,其中存储的消息与正在测试的消息相同。在这种情况下,新消息属于该集合,并被称为被接受。
- 找到一个空单元。在这种情况下,新消息不属于该集合,并被称为被拒绝。
两种允许误差的哈希编码方法 #
方法 1 是以自然的方式从传统的无错误方法派生的。哈希区域像以前一样被组织成单元,但单元更小,包含代码而不是整个消息。代码是从消息生成的,其大小取决于允许的错误分数。直观上,可以看出单元大小应该随着允许的错误分数变小而增加。当错误分数足够小时(大约为 2-b),单元将足够大以包含整个消息本身,从而不会产生错误。如果 P 表示允许的错误分数,则假设 1 » P » 2-b。
确定了单元的大小(例如 c < b),选择该大小以使预期的错误分数接近且小于 P,哈希区域被组织成 c 位的单元。然后将每个消息编码成一个 c 位代码(不一定唯一),并且以类似于传统无错误方法中使用的方式存储和测试这些代码。和以前一样,每个代码的第一位设置为 1。由于代码不是唯一的,就像原始消息一样,可能会出现委托错误。
方法 2 完全摆脱了将哈希区域组织成单元的传统概念。哈希区域被视为 N 个单独可寻址的位,地址为 0 到 N - 1。假设哈希区域中的所有位首先设置为 0。接下来,要存储的集合中的每个消息都被哈希编码成多个不同的位地址,例如 a1、a2、…、ad。最后,所有由 a1 到 ad 寻址的 d 位都设置为 1。
要测试新消息,将以与存储消息相同的方式生成一系列 d 位地址,例如 a1、a2、…、ad。如果所有 d 位都为 1,则新消息被接受。如果这些位中的任何一位为零,则该消息被拒绝。
直观上,可以看出,在达到收益递减点之前,d 越大,预期的错误分数就越小。当将 d 增加 1 导致哈希字段中 1 位的分数增长过大时,就会出现收益递减点。稍后本文将表明,当哈希字段中一半位为 1,一半位为 0 时,每个访问位为 1 的先验可能性增加超过了添加要测试的额外位的效果。因此,对于任何给定的哈希字段大小 N,都存在一个最小可能的预期错误分数,因此方法 2 排除了通过修改方法 1 以获得非常小的允许错误分数而可能实现的无错误性能。
计算因素 #
允许的错误分数。 将根据允许一些消息被错误地识别为给定消息集的成员可以减少哈希区域的大小来分析此因素。我们用以下公式表示错误分数: $$ P = \frac{n_a - n}{n_t - n} $$ (1)
其中:
- $$n_a$$ 是消息空间中将被接受为给定集合成员的消息数量
- $$n$$ 是给定集合中的消息数量
- $$n_t$$ 是消息空间中不同消息的总数
空间。 基本空间因素是哈希区域中的位数 N。通过分析更改 N 值对时间因素的影响,稍后将引入一个合适的标准化空间因素度量。使用此标准化度量将把由于给定消息集中消息数量和允许的错误分数而对时间产生的影响与由于哈希区域大小而对时间产生的影响分开。这种效果分离将允许更清晰地呈现空间/时间权衡。
时间。 时间因素是将消息拒绝为给定集合成员所需的平均时间。在测量这个因素时,使用的单位是在哈希区域中计算单个位地址、访问寻址位和对位内容进行适当测试所需的时间。
对于传统的哈希编码方法,测试是比较哈希区域中的寻址位与消息中相应的位。对于方法 1,测试是比较哈希区域位与从消息派生的相应代码位。对于方法 2,测试只是简单地确定哈希区域位的内容;例如,它是 1 吗?对于以下分析,假设三个方法和哈希区域中的所有位的时间单位相同1。
以这些单位测量的時間因素称为归一化时间度量,并且将针对此因素分析空间/时间权衡。归一化时间度量为:
$$ T = \text{mean} \left( t_i \right)_{m_i \in a} $$
(2)
其中:
- M 是给定的消息集
- a 是被识别(正确或错误)为 M 成员的消息集
- g 是被识别为非 M 成员的消息集
- $$m_i$$ 是第 i 条消息
- $$t_i$$ 是拒绝第 i 条消息所需的时间
传统哈希编码方法的分析 #
哈希区域有 N 位,并被组织成 h 个单元,每个单元 b + 1 位,其中 n 个单元填充了 M 中的 n 条消息。让 Φ 表示为空的单元的分数。然后
$$ \frac{h - n}{h} = \frac{N - n \cdot (b + 1)}{N} = \Phi - \frac{h}{N} $$ (3)
求解 N 得到
$$ N = \frac{n \cdot (b + 1)}{1 - \Phi} $$ (4)
现在让我们计算归一化时间度量 T。T 表示在典型拒绝过程中要测试的预期位数。T 也等于在访问和放弃非空单元后要测试的预期位数。也就是说,如果一个哈希寻址单元包含一条与要测试的消息不同的消息,那么平均来说,在测试了 E 位之后就会发现这一点。然后,该过程实际上又重新开始。
由于 Φ 表示为空的单元的分数,因此访问非空单元的概率为 (1 - Φ),访问空单元的概率为 Φ。如果访问一个非空单元,则要测试的预期位数为 E + T,因为 E 表示拒绝访问的非空单元时要测试的预期位数,T 表示重复该过程时要测试的预期位数。如果访问一个空单元,则只测试一位即可发现这一事实。因此
$$ T = (1 - \Phi) \cdot (E + T) + \Phi $$ (5)
为了计算 E 的值,我们注意到,在给定单元包含一条与要测试的消息不同的消息的条件下,单元的前 x 位与要测试的消息的位匹配,而第 (x + 1) 位不匹配的条件概率为 $$(\frac{1}{2})^x$$。(读者应该记住,消息的第一位始终与非空单元的第一位匹配,因此指数为 x 而不是 x + 1,否则就是这种情况。)因此,对于 b » 1,E 的期望值近似为以下总和:
$$ \sum_{x=1}^{\infty} (x + 1) \cdot (\frac{1}{2})^x = 3 $$ (6)
因此
$$ T = \frac{3}{\Phi} - 2 $$ (7)
$$ N = \frac{n \cdot (b + 1) \cdot (T + 2)}{T - 1} $$ (8)
方程 (8) 表示传统哈希编码方法的空间/时间权衡。
方法 1 的分析 #
哈希区域包含 N’ 位,并被组织成 c 位的单元。以类似于传统方法的方式,我们建立以下方程式:
$$ \Phi’ = \frac{N’ - n \cdot c}{N’} $$ (9) - 空单元的分数。
$$ N’ = \frac{n \cdot c}{1 - \Phi’} $$ (10)
$$ T’ = \frac{3}{\Phi’} - 2 $$ (11)
$$ N’ = \frac{n \cdot c \cdot (T’ + 2)}{T’ - 1} $$ (12)
剩下的就是根据 c 和 T’ 以及根据 N’ 和 T’ 推导出相应预期错误分数 P’ 的关系。
一条要测试的消息,它不是消息集 M 的成员,当满足以下条件时,将被错误地接受为 M 的成员:
(1) 从测试消息生成的一系列哈希地址之一包含与从测试消息生成的相同的代码,例如 C;并且 (2) 这样的哈希地址是在序列中比某个空单元的哈希地址更早生成的。
然后,被错误接受的非 M 成员的测试消息的预期分数为
$$ P’ = \frac{(\frac{1}{2})^{c-1}}{\Phi’} $$ (13)
因此
$$ c = - log_2P’ + 1 + log_2(\frac{T’ + 2}{T’ - 1}) $$ (14)
$$ N’ = n \cdot (-log_2P’ + 1 + log_2(\frac{T’ + 2}{T’ - 1})) \cdot \frac{T’ + 2}{T’ - 1} $$ (15)
方程 (15) 表示方法 1 的所有三个计算因素之间的权衡。
方法 2 的分析 #
让 Φ" 表示在存储了 n 条消息后,N" 位哈希区域中仍设置为 0 的位的预期比例,其中 d 是为给定集合中的每条消息设置为 1 的不同位数。
$$ \Phi" = (1 - \frac{d}{N"})^n $$ (16)
如果测试的所有 d 位都为 1,则不在给定集合中的消息将被错误接受。然后,导致此类错误的非 M 成员的测试消息的预期分数为
$$ P" = (1 - \Phi")^d $$ (17)
假设 d « N",当然就是这种情况,我们取等式 (16) 两边的以 2 为底的对数,得到近似
$$ log_2\Phi" = log_2(1 - \frac{d}{N"})^n $$
$$ = -n \cdot (\frac{d}{N"}) \cdot log_2e $$
因此
$$ N" = \frac{n \cdot (-log_2P") \cdot log_2e}{log_2\Phi"} $$ (19)
我们现在推导出归一化时间度量 T" 的关系。当测试的前 x - 1 位为 1,而测试的第 x 位为 0 时,将测试 x 位。这发生的概率为 $$ \Phi" \cdot (1 - \Phi")^{x-1}$$。对于 P" « 1 和 d » 1,T" 的近似值(每个被拒绝的测试消息的测试位数的期望值)为
$$ T" = \sum_{x=1}^{\infty} x \cdot \Phi" \cdot (1 - \Phi")^{x-1} = \frac{1}{\Phi"} $$ (20)
因此
$$ N" = \frac{n \cdot (-log_2P") \cdot log_2e}{log_2(\frac{1}{T"}) \cdot log_2(1 - \frac{1}{T"})} $$ (21)
方程 (21) 表示方法 2 的三个计算因素之间的权衡。
方法 1 和方法 2 的比较 #
为了比较方法 1 和方法 2 之间的相对空间/时间权衡,引入一个归一化空间度量会很有用,
$$ S = \frac{N}{-n \cdot log_2P} $$ (22)
S 被标准化以消除给定消息集的大小 n 和允许的错误分数 P 的影响。将关系 (22) 代入等式 (15) 和 (21) 得到
$$ S’ = (-log_2P’ + 1 + log_2(\frac{T’ + 2}{T’ - 1})) \cdot \frac{T’ + 2}{T’ - 1} $$ (23)
$$ S" = \frac{log_2e}{log_2(\frac{1}{T"}) \cdot log_2(1 - \frac{1}{T"})} $$ (24)
我们注意到 $$S’ > \frac{T’ + 2}{T’ - 1}$$,并且
$$ \lim_{\Phi’ \to 0} S’ = \frac{T’ + 2}{T’ - 1} $$ (25)
可以通过检查图 1 直接看到方法 2 比方法 1 的优越性,图 1 是等式 (24) 的 S 与 T 曲线和下限极限方程 (25) 的图形。图 1 中的曲线说明了两种方法的空间/时间权衡,假设预期错误分数 P 和消息数量 n 的值固定。
对于方法 2,T" 的增加对应于 Φ" 的减少,Φ" 是所有 n 条消息都被哈希编码后哈希字段中 0 位的分数。为了保持 P 的固定值,Φ" 的这种减少对应于每个消息的测试位数 d 的增加,以及对哈希区域大小 N" 的适当调整。S" 与哈希区域大小 N" 成正比,如等式 (22) 所示。随着 T" 的增加,相应地,Φ" 减少,S 和 N" 减少,直到达到收益递减点。这个收益递减点在图 1 中说明,其中 S" 在 $$\frac{1}{T"} = 1 - \frac{1}{T"}$$ 时最小,即在 T" = 2 时。
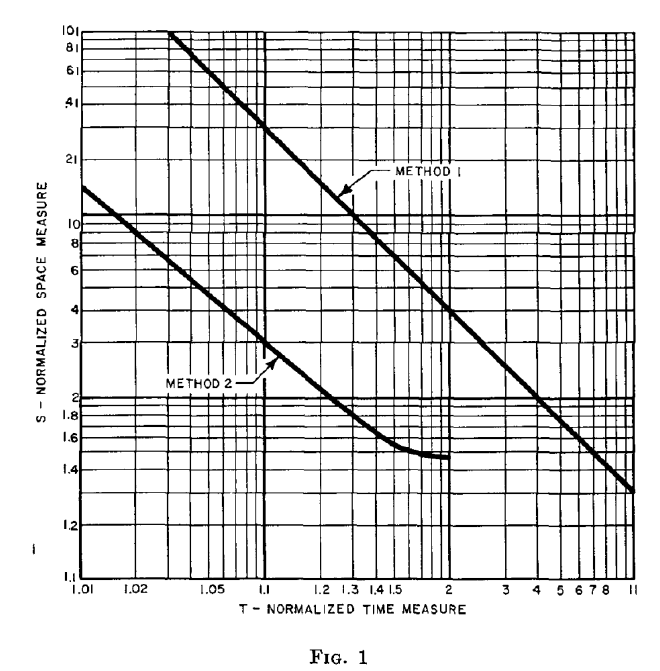
由于 $$\Phi" = \frac{1}{T"}$$,这意味着可以使用方法 2 的最小哈希区域发生在一半位为 1 而另一半位为 0 时。对应于 T" = 2 的 S" 值为 $$S" = log_2e = 1.47$$。
连字符示例应用程序的分析 #
在本节中,我们将计算一个名义大小的哈希区域,用于解决示例自动连字符问题。由于我们已经得出结论,方法 2 比方法 1 更好,因此我们将传统方法与方法 2 进行比较。
让我们假设程序要连字符大约 500,000 个单词,其中 450,000 个单词可以通过应用一些简单的规则来连字符。其他 50,000 个单词需要参考字典。可以合理地估计,使用传统的哈希编码方法表示这 50,000 个单词中的每一个平均至少需要 19 位。如果我们假设时间因素 T = 4 是可以接受的,那么我们从等式 (9) 发现哈希区域的大小为 2,000,000 位。对于实际的核心包含哈希区域来说,这可能太大了。通过使用允许误差频率为 P = 1/16 的方法 2,并通过让 T = 2 使用最小的哈希区域,我们从等式 (22) 看到,可以使用小于 300,000 位的哈希区域来解决问题,这个大小很可能适合核心哈希区域。
选择 P 为 1/16 时,对于大约 50,000 + 450,000/16 ≈ 78,000 个要连字符的 500,000 个单词,即大约 16% 的情况,需要访问磁盘驻留字典。与使用完全磁盘驻留哈希区域和字典的典型传统方法相比,这减少了 84% 的磁盘访问次数。
表 I 显示了对 P 值的替代选择如何影响核心驻留哈希区域的大小以及与“典型传统方法”相比节省的磁盘访问百分比。
| P = Allowable Fraction of Errors | N = Size of Hash Area (Bits) | Disk Accesses Saved |
|---|---|---|
| 1/2 | 72,800 | 45.0% |
| 1/4 | 145,600 | 67.5% |
| 1/8 | 218,400 | 78.7% |
| 1/16 | 291,200 | 84.4% |
| 1/32 | 364,000 | 87.2% |
| 1/64 | 509,800 | 88.5% |
P = 允许的错误分数 N = 哈希区域大小(位) 节省的磁盘访问次数
致谢 #
作者要感谢奥利弗·塞尔弗里奇先生在撰写本文时提供的许多有益建议。
参考文献 #
- BATSON, A. 符号表组织。ACM 通讯,8, 2(1965 年 2 月),111-112。
- MAURER, W. D. 用于分散存储的改进哈希码。ACM 通讯,11, 1(1968 年 1 月),35-38。
- MORRIS, R. 分散存储技术。ACM 通讯,11, 1(1968 年 1 月),38-44。
